
ちょっとした趣味です(笑)。興味のある方はどうぞ。
チェバの定理とは、「三角形」と「点」の関係性の定理です。
$\bigtriangleup ABC$と点$D$があります。
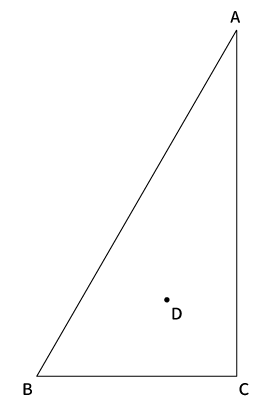
下図のように「$AD$を通る直線」と「$BC$」との交点を$E$、「$BD$を通る直線」と「$AC$」との交点を$F$、「$CD$を通る直線」と「$AB$」との交点を$G$とします。
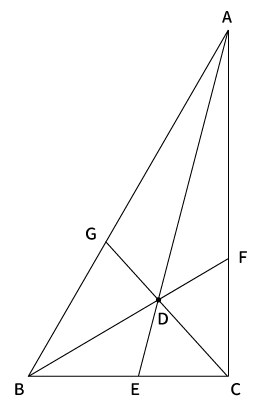
このとき、$\displaystyle \frac{AG}{BG} \frac{BE}{CE} \frac{CF}{AF} = 1$となります。これがチェバの定理です。
※上の画像は直角三角形ですが、「どんな三角形」でも「どの位置の点(三角形の頂点以外)」でも成り立ちます
では、$\displaystyle \frac{AG}{BG} \frac{BE}{CE} \frac{CF}{AF} = 1$の式が成り立つか証明したいと思います。もし、不明点・質問等ありましたらお気軽にコメントください^^
スポンサーリンク証明のざっくりとした流れ
なんとなくでもイメージしやすいように、先にざっくりとした流れを見ておきます。
$\bigtriangleup ABC$と点$D$からできる↓この2つの三角形(赤と青)とか、
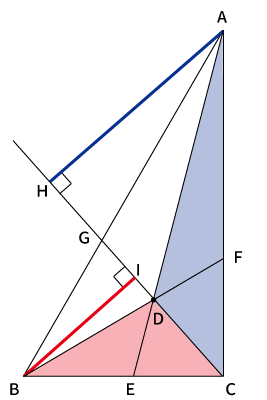
↓この2つの三角形とか(赤と青)、
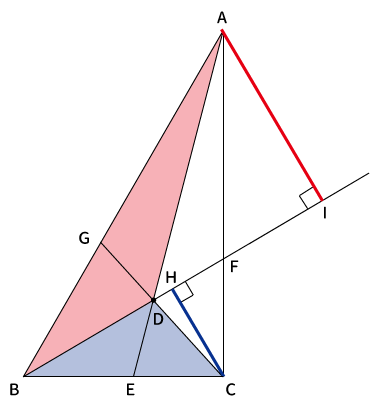
↓この2つの三角形(赤と青)とかが、それぞれ相似になっていて、

辺や面積の比をうまく考えると、$\displaystyle \frac{S_{acd}}{S_{bcd}}=\frac{AG}{BG}$、$\displaystyle \frac{S_{bcd}}{S_{abd}}=\frac{CF}{AF}$、$\displaystyle \frac{S_{abd}}{S_{acd}}=\frac{BE}{CE}$となるので、それぞれ掛け合わせると、チェバの定理の完成です。
$\bigtriangleup ACD$の面積を$S_{acd}$、$\bigtriangleup BCD$の面積を$S_{bcd}$、$\bigtriangleup ABD$の面積を$S_{abd}$とします。
それでは、詳しく見ていきます。
$\bigtriangleup ACD$と$\bigtriangleup BCD$から分かること
まずは、$\bigtriangleup ACD$と$\bigtriangleup BCD$の関係性を調べていきます。
$\bigtriangleup ACD$と$\bigtriangleup BCD$の面積
$\bigtriangleup ACD$(青)と$\bigtriangleup BCD$(赤)の面積を考えていきます。
面積を求めるには底辺と高さが必要ですね。それぞれ見ていきましょう。
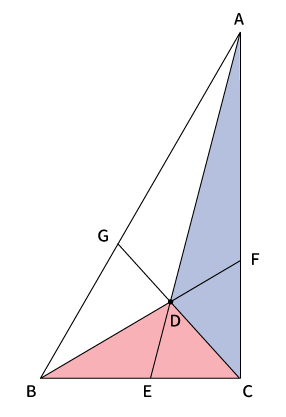
底辺
$\bigtriangleup ACD$と$\bigtriangleup BCD$の共通の辺$CD$を底辺と考えます。
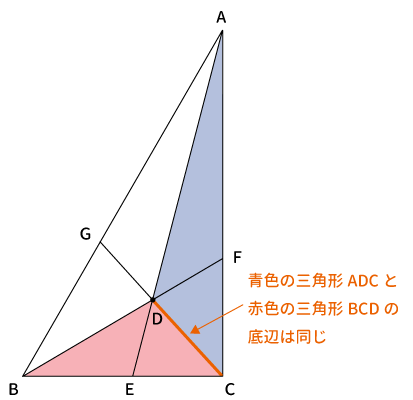
高さ
続いて各三角形の高さを考えます。
青い三角形も赤い三角形も同じ方法で高さを求められます。では、どのように求めるか見ていきます。
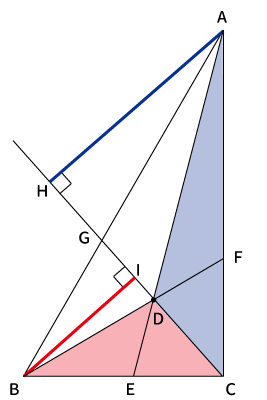
最初に下図のように$CD$を延長します。
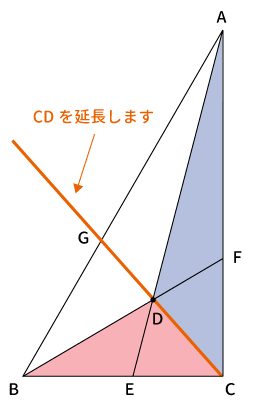
続いて、頂点$A$から$CD$を延長した線に対して垂線を引き、その交点を$H$とすると、青色の三角形の高さが$AH$となります。
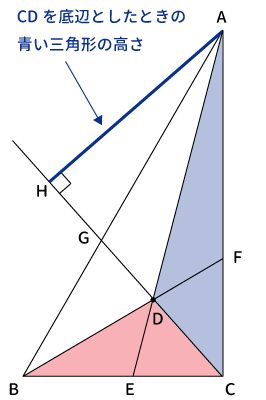
同様に、頂点$B$から$CD$を延長した線に対して垂線を引き、その交点を$I$とすると、赤色の三角形の高さが$BI$となります。

これで、青い三角形と赤い三角形に対して、$CD$を底辺としたときの各高さがどれか分かりました。
面積
以上より、$\bigtriangleup ACD$の面積を$S_{acd}$、$\bigtriangleup BCD$の面積を$S_{bcd}$とすると、各三角形の面積は下記のようになります。
青色の$\bigtriangleup ACD$の面積$\displaystyle S_{acd} = \frac{CD・AH}{2}$
赤色の$\bigtriangleup BCD$の面積は$\displaystyle S_{bcd} = \frac{CD・BI}{2}$
実は、今求めた各三角形の高さ$AH$と$BI$と$AG$、$BG$には面白い関係性があります。
高さ$AH$、$BI$と$AG$、$BG$との関係性
高さ$AH$、$BI$と$AG$、$BG$との関係性を調べるために、$\bigtriangleup AGH$と$\bigtriangleup BGI$の関係性を見ていきます。

$\bigtriangleup AGH$と$\bigtriangleup BGI$の$\angle AHG$、$\angle BIG$はともに$90^{\circ}$です。どちらも垂線を引いたものなので当たり前ですね。
また、$\angle AGH$と$\angle BGI$は対頂角(向かい合う角)なので、等しいです。
よって、$\angle AHG = \angle BIG$、$\angle AGH = \angle BGI$なので、$\bigtriangleup AGH$と$\bigtriangleup BGI$は2角が等しい。つまり、$\bigtriangleup AGH$と$\bigtriangleup BGI$は相似であることが分かりました。
$\bigtriangleup AGH$と$\bigtriangleup BGI$は相似より、各辺の比は等しい
$\bigtriangleup AGH$と$\bigtriangleup BGI$は相似より、各辺の比は等しくなります。
つまり、$AH$と$BI$、$AG$と$BG$、残りの$GH$と$GI$がそれぞれ同じ比率になります。

関係性
よって、$AH:BI=AG:BG$となるので、$AH・BG=BI・AG$が成り立ちます。従って、高さ$AH$、$BI$と$AG$、$BG$には、$\displaystyle \frac{AH}{BI}=\frac{AG}{BG}$という関係性があることが分かりました。
$\bigtriangleup ADC$と$\bigtriangleup BCD$の面積比も同じ
高さ$AH$、$BI$と$AG$、$BG$には、$\displaystyle \frac{AH}{BI}=\frac{AG}{BG}$という関係性が分かりました。この関係式を変形すると、面積比も分かります。
$\displaystyle \frac{AH}{BI}=\frac{AG}{BG}$の左辺に$\displaystyle \frac{\frac{CD}{2}}{\frac{CD}{2}}$を掛けます。※$\displaystyle \frac{\frac{CD}{2}}{\frac{CD}{2}}=1$なので、掛けても問題ありませんね
(左辺)$\displaystyle = \frac{AH}{BI} \times \frac{\frac{CD}{2}}{\frac{CD}{2}}=\frac{\frac{CD・AH}{2}}{\frac{CD・BI}{2}}$
ここで、下図、青色の三角形と赤色の三角形の面積を思い出してください。
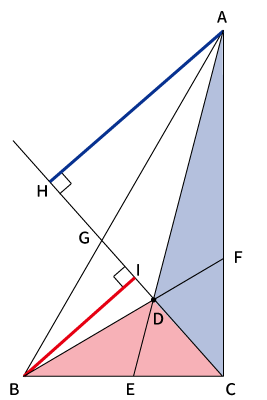
青と赤の三角形の面積は下記の通りでしたよね。
青色の$\bigtriangleup ADC$の面積$\displaystyle \color{blue} S_{adc} = \frac{CD・AH}{2}$
赤色の$\bigtriangleup BCD$の面積は$\displaystyle \color{red} S_{bcd} = \frac{CD・BI}{2}$
これは、先ほどの左辺の分母と分子がそれぞれの面積になっています。
(左辺)$\displaystyle =\frac{\color{blue} \frac{CD・AH}{2}}{\color{red} \frac{CD・BI}{2}}$
よって、
(左辺)$\displaystyle = \frac{\frac{CD・AH}{2}}{\frac{CD・BI}{2}} = \frac{S_{adc}}{S_{bcd}}$
少しまとめます
少しややこしくなってきましたので、少しまとめます。
まず、相似関係より$\displaystyle \frac{AH}{BI}=\frac{AG}{BG}$が分かりました。ここから先ほどまでの計算の流れを式にしますね。
$\displaystyle \frac{AH}{BI} =\frac{AH}{BI} \times \frac{\frac{CD}{2}}{\frac{CD}{2}}$
$\displaystyle =\frac{\frac{CD・AH}{2}}{\frac{CD・BI}{2}}$
$\displaystyle =\frac{S_{adc}}{S_{bcd}}$
$\displaystyle =\frac{AG}{BG}$
つまり、$\displaystyle \frac{AH}{BI}=\frac{S_{adc}}{S_{bcd}}=\frac{AG}{BG}$

青と赤の三角形の面積と$AG$、$BG$との関係性$\displaystyle \frac{S_{adc}}{S_{bcd}}=\frac{AG}{BG}$が分かりました。
スポンサーリンク
$\bigtriangleup BCD$と$\bigtriangleup ABD$から分かること
「$\bigtriangleup ADC$と$\bigtriangleup BCD$から分かること」と全く同じ手順を行うことで、
青と赤の三角形の面積と$AF$、$CF$との関係性$\displaystyle \frac{S_{bcd}}{S_{abd}}=\frac{CF}{AF}$が分かりました。
※同じ手順ですが、詳細を書いてほしい場合は、コメントくださいね
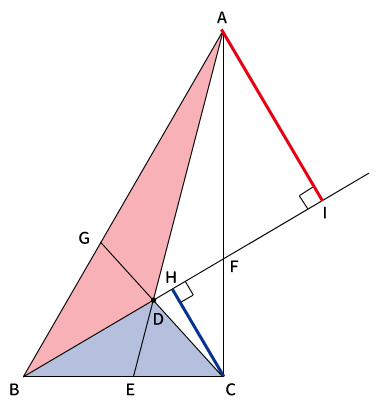
$\bigtriangleup ABD$と$\bigtriangleup ACD$から分かること
「$\bigtriangleup ACD$と$\bigtriangleup BCD$から分かること」と全く同じ手順を行うことで、
青と赤の三角形の面積と$AF$、$CF$との関係性$\displaystyle \frac{S_{abd}}{S_{acd}}=\frac{BE}{CE}$が分かりました。
※同じ手順ですが、詳細を書いてほしい場合は、コメントくださいね

$\bigtriangleup ACD$と$\bigtriangleup BCD$と$\bigtriangleup ABD$より
以上より、下記3つの式を得ました。
$\displaystyle \frac{S_{acd}}{S_{bcd}}=\frac{AG}{BG}$・・・( i )
$\displaystyle \frac{S_{bcd}}{S_{abd}}=\frac{CF}{AF}$・・・( ii )
$\displaystyle \frac{S_{abd}}{S_{acd}}=\frac{BE}{CE}$・・・( iii )
( i ) と ( ii )の各辺を掛けます。
$\displaystyle \frac{S_{acd}}{S_{bcd}}・\frac{S_{bcd}}{S_{abd}}=\frac{AG}{BG} ・\frac{CF}{AF}$
$\displaystyle \frac{S_{acd}}{S_{abd}}=\frac{AG}{BG} ・\frac{CF}{AF}$・・・ ( iv )
( iv ) と ( iii ) の各辺を掛けます。
$\displaystyle \frac{S_{acd}}{S_{abd}}・\frac{S_{abd}}{S_{acd}}=\frac{AG}{BG} ・\frac{CF}{AF}・\frac{BE}{CE}$
$\displaystyle 1=\frac{AG}{BG} ・\frac{CF}{AF}・\frac{BE}{CE}$
以上で証明終了です。
参考(入れ替えなど不要です)
$\displaystyle 1=\frac{AG}{BG} ・\frac{CF}{AF}・\frac{BE}{CE}$を最初に定理を紹介した、下記に合わせておきます。
$\displaystyle \frac{AG}{BG} \frac{BE}{CE} \frac{CF}{AF} = 1$
$\displaystyle 1=\frac{AG}{BG} ・\frac{CF}{AF}・\frac{BE}{CE}$
両辺入れ替えます。
$\displaystyle \frac{AG}{BG} ・\frac{CF}{AF}・\frac{BE}{CE} = 1$
$\displaystyle \frac{CF}{AF}$と$\displaystyle \frac{BE}{CE}$を入れ替えます。
$\displaystyle \frac{AG}{BG} ・\frac{BE}{CE}・\frac{CF}{AF} = 1$
拡張
外部に点がある場合も別途証明してみました。興味のある方はこちら→「【チェバの定理の拡張】外部に点がある場合を証明する」をご覧ください。
まとめ
三角形と点によって引かれた線によってできた3つの三角形の面積をうまく使うことで、チェバの定理を証明することができました。
ちなみに直角三角形が作図しやすかったので、そちらを例に進めましたが、どのような三角形でも同じ手順で同じ結果が得られると思います。
もし、試してほしい形の三角形があれば、コメントください。検証してみます。
それでは、最後までお読みいただきありがとうございました!
キーワード
気になる人はGoogle検索で調べてみてね。
チェバの定理、三角形、相似、対頂角
スポンサーリンク

