
内部に点がある場合のチェバの定理は「チェバの定理とは?図解!分かりやすく証明」をご覧ください。
チェバの定理とは、「三角形」と「点」の関係性の定理です。今回はこの「点」が「三角形」の外にある場合を証明したいと思います。
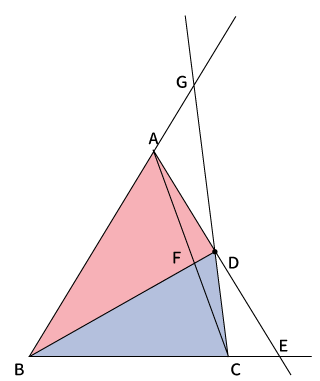
$\bigtriangleup ABC$と点$D$があります。
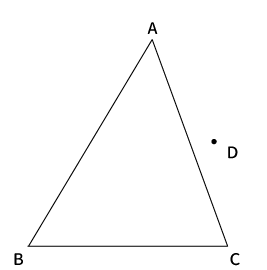
下図のように$AD$、$BD$、$CD$を引きます。
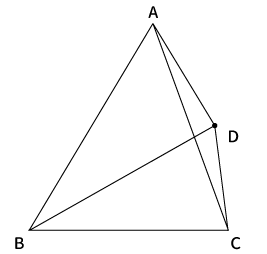
この線分を引いただけだと、$AD$、$CD$には三角形の辺との交点がありません。
よって、$AB$と$BC$を延長して、$AD$を通る直線と$BC$の延長線との交点を$E$、$BD$を通る直線と$AC$との交点を$F$、$CD$を通る直線と$AB$の延長線との交点を$G$とします。
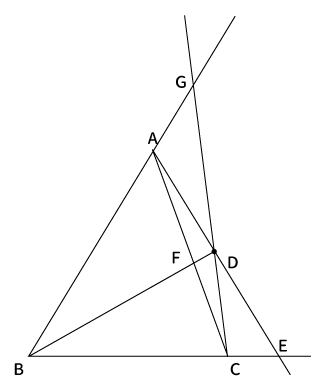
このとき、$\displaystyle \frac{AG}{BG} \frac{BE}{CE} \frac{CF}{AF} = 1$となります。これが点が三角形の外部にある場合のチェバの定理です。
※上図の三角形以外の三角形でも、どの位置の点(三角形の頂点以外)でも成り立ちます
では、点が外部にある場合でも$\displaystyle \frac{AG}{BG} \frac{BE}{CE} \frac{CF}{AF} = 1$の式が成り立つことを証明したいと思います。
もし、不明点・質問等ありましたらお気軽にコメントください^^
スポンサーリンク証明のざっくりとした流れ
なんとなくでもイメージしやすいように、先にざっくりとした流れを見ておきます。
$\bigtriangleup ABC$と点$D$からできる↓この2つの三角形(赤と青)とか、
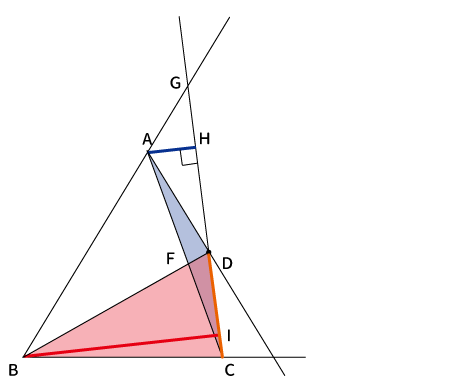
↓この2つの三角形(赤と青)とか、
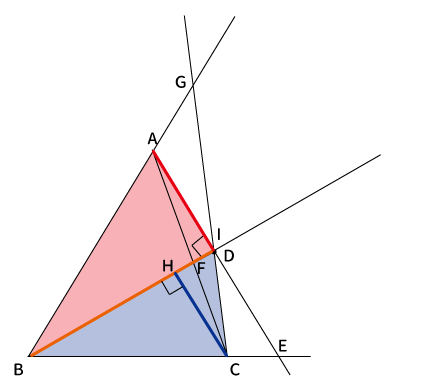
↓この2つの三角形(赤と青)とかが、それぞれ相似になっていて、
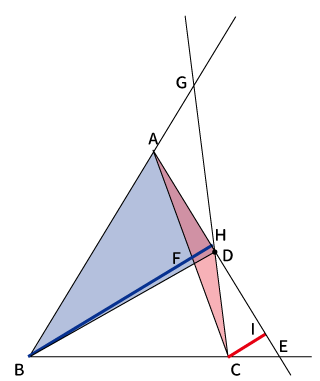
辺や面積の比をうまく考えると、$\displaystyle \frac{S_{acd}}{S_{bcd}}=\frac{AG}{BG}$、$\displaystyle \frac{S_{bcd}}{S_{abd}}=\frac{CF}{AF}$、$\displaystyle \frac{S_{abd}}{S_{acd}}=\frac{BE}{CE}$となるので、それぞれ掛け合わせると、なんとチェバの定理の完成です。
$\bigtriangleup ACD$の面積を$S_{acd}$、$\bigtriangleup BCD$の面積を$S_{bcd}$、$\bigtriangleup ABD$の面積を$S_{abd}$とします。
それでは、詳しく見ていきます。
$\bigtriangleup ACD$と$\bigtriangleup BCD$から分かること
まずは、$\bigtriangleup ACD$と$\bigtriangleup BCD$の関係性を調べていきます。
$\bigtriangleup ACD$と$\bigtriangleup BCD$の面積
まず、$\bigtriangleup ACD$(青)と$\bigtriangleup BCD$(赤)の面積を考えていきます。$\bigtriangleup ACD$(青)の面積を$S_{acd}$、$\bigtriangleup BCD$(赤)の面積を$S_{bcd}$とします。
さて、面積を求めるには底辺と高さが必要ですね。それぞれ見ていきましょう。

底辺
$\bigtriangleup ACD$と$\bigtriangleup BCD$の共通の辺$CD$を底辺と考えます。
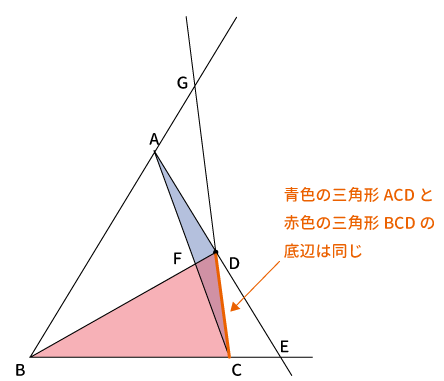
高さ
続いて各三角形の高さを考えます。
青い三角形も赤い三角形も同じ方法で高さを求められます。
頂点$A$から$CD$を延長した線($CG$)に対して垂線を引き、その交点を$H$とすると、青色の三角形の高さは$AH$となります。
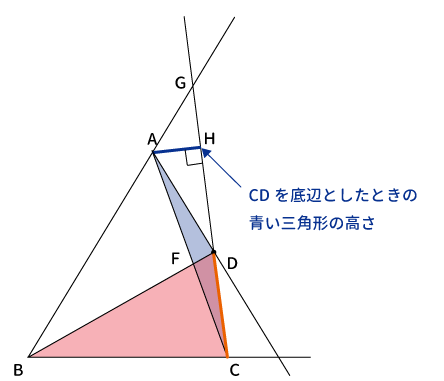
同様に、頂点$B$から$CD$に対して垂線を引き、その交点を$I$とすると、赤色の三角形の高さ$BI$となります。

これで、青い三角形と赤い三角形に対して、$CD$を底辺としたときの各高さが$AH$、$BI$だと分かりました。

面積
以上より、各三角形の面積は下記のようになります。
青色の$\bigtriangleup ACD$の面積$\displaystyle S_{acd} = \frac{CD・AH}{2}$
赤色の$\bigtriangleup BCD$の面積は$\displaystyle S_{bcd} = \frac{CD・BI}{2}$
実は、今求めた各三角形の高さ$AH$と$BI$と$AG$、$BG$には面白い関係性があります。
高さ$AH$、$BI$と$AG$、$BG$との関係性
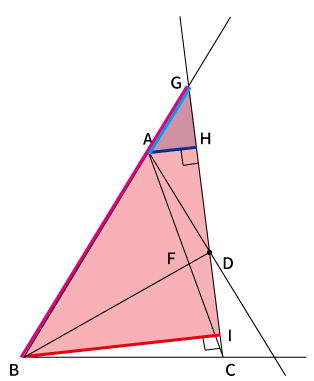
高さ$AH$、$BI$と$AG$、$BG$との関係性を調べるために、$\bigtriangleup AGH$と$\bigtriangleup BGI$の関係性を見ていきます。
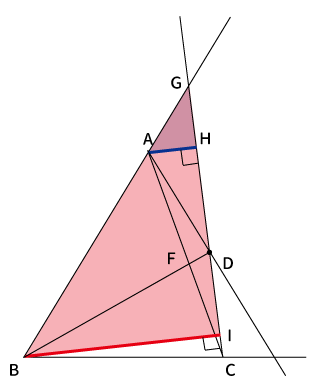
$\bigtriangleup AGH$と$\bigtriangleup BGI$の$\angle AHG$、$\angle BIG$はともに$90^{\circ}$です。そのように作図したので当前ですね。
また、$\angle AGH$と$\angle BGI$は同じ角度を指しています。
よって、$\angle AHG = \angle BIG$、$\angle AGH = \angle BGI$なので、$\bigtriangleup AGH$と$\bigtriangleup BGI$は2角が等しい。つまり、$\bigtriangleup AGH$と$\bigtriangleup BGI$は相似な図形だと分かりました。
$\bigtriangleup AGH$と$\bigtriangleup BGI$は相似より、各辺の比は等しい
$\bigtriangleup AGH$と$\bigtriangleup BGI$は相似より、各辺の比は等しくなります。
$AH$と$BI$、$AG$と$BG$、残りの$GH$と$GI$がそれぞれ同じ比率になります。
関係性
よって、$AH:BI=AG:BG$となるので、$AH・BG=BI・AG$が成り立ちます。従って、高さ$AH$、$BI$と$AG$、$BG$には、$\displaystyle \frac{AH}{BI}=\frac{AG}{BG}$という関係性があることが分かりました。
$\bigtriangleup ACD$と$\bigtriangleup BCD$の面積比も同じ
高さ$AH$、$BI$と$AG$、$BG$には、$\displaystyle \frac{AH}{BI}=\frac{AG}{BG}$という関係性が分かりました。この関係式を変形することで、面積比も知ることができます。
$\displaystyle \frac{AH}{BI}=\frac{AG}{BG}$の左辺に$\displaystyle \frac{\frac{CD}{2}}{\frac{CD}{2}}$を掛けます。※$\displaystyle \frac{\frac{CD}{2}}{\frac{CD}{2}}=1$なので、掛けても問題ありませんね
(左辺)$\displaystyle = \frac{AH}{BI} \times \frac{\frac{CD}{2}}{\frac{CD}{2}}=\frac{\frac{CD・AH}{2}}{\frac{CD・BI}{2}}$
ここで、下図、青色の三角形と赤色の三角形の面積を思い出してください。左辺の分母と分子がそれぞれの面積になっていますね。

青と赤の三角形の面積は下記の通りでしたよね。
青色の$\bigtriangleup ACD$の面積$\displaystyle \color{blue} S_{acd} = \frac{CD・AH}{2}$
赤色の$\bigtriangleup BCD$の面積は$\displaystyle \color{red} S_{bcd} = \frac{CD・BI}{2}$
これは、先ほどの左辺の分母と分子がそれぞれの面積になっています。
(左辺)$\displaystyle =\frac{\color{blue} \frac{CD・AH}{2}}{\color{red} \frac{CD・BI}{2}}$
よって、
(左辺)$\displaystyle = \frac{\frac{CD・AH}{2}}{\frac{CD・BI}{2}} = \frac{S_{acd}}{S_{bcd}}$
少しまとめます
少しややこしくなってきましたので、少しまとめます。
まず、相似関係より$\displaystyle \frac{AH}{BI}=\frac{AG}{BG}$が分かりました。ここから先ほどまでの計算の流れを式にしますね。
$\displaystyle \frac{AH}{BI} =\frac{AH}{BI} \times \frac{\frac{CD}{2}}{\frac{CD}{2}}$
$\displaystyle =\frac{\frac{CD・AH}{2}}{\frac{CD・BI}{2}}$
$\displaystyle =\frac{S_{adc}}{S_{bcd}}$
$\displaystyle =\frac{AG}{BG}$
つまり、$\displaystyle \frac{AH}{BI}=\frac{S_{adc}}{S_{bcd}}=\frac{AG}{BG}$

青と赤の三角形の面積と$AG$、$BG$との関係性$\displaystyle \frac{S_{adc}}{S_{bcd}}=\frac{AG}{BG}$が分かりました。
スポンサーリンク
$\bigtriangleup BCD$と$\bigtriangleup ABD$から分かること
次に、$\bigtriangleup BCD$と$\bigtriangleup ABD$の関係性を調べていきます。
$\bigtriangleup BCD$と$\bigtriangleup ABD$の面積
まず、青色の$\bigtriangleup BCD$と赤色の$\bigtriangleup ABD$の面積を考えていきます。青色の$\bigtriangleup BCD$の面積を$S_{bcd}$、赤色の$\bigtriangleup ABD$の面積を$S_{abd}$とします。
さて、面積を求めるには底辺と高さが必要ですね。それぞれ見ていきましょう。
底辺
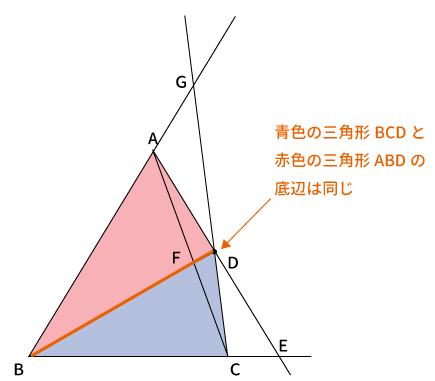
$\bigtriangleup BCD$と$\bigtriangleup ABD$の共通の辺$BD$を底辺と考えます。
高さ
続いて各三角形の高さを考えます。
青い三角形も赤い三角形も同じ方法で高さを求められます。
頂点$C$から$BD$に対して垂線を引き、その交点を$H$とすると、青色の三角形の高さが$AH$となります。
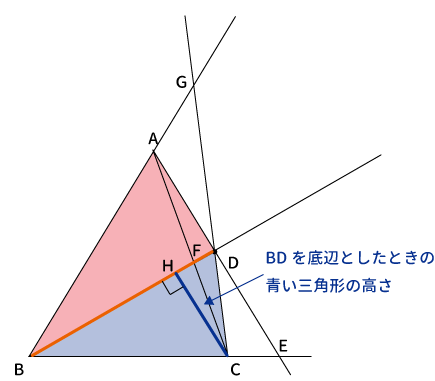
同様に、頂点$A$から$BD$に対して垂線を引き、その交点を$I$とすると、赤色の三角形の高さが$BI$になります。
 \
\
これで、青い三角形と赤い三角形に対して、$BD$を底辺としたときの各高さが分かりました。

面積
以上より、各三角形の面積は下記のようになります。
青色の$\bigtriangleup BCD$の面積$\displaystyle S_{bcd} = \frac{BD・CH}{2}$
赤色の$\bigtriangleup ABD$の面積は$\displaystyle S_{abd} = \frac{BD・AI}{2}$
実は、今求めた各三角形の高さ$CH$と$AI$と$CF$、$AF$には面白い関係性があります。
高さ$AH$、$BI$と$CF$、$AF$との関係性
高さ$AH$、$BI$と$CF$、$AF$との関係性を調べるために、$\bigtriangleup CFH$と$\bigtriangleup AFI$の関係性を見ていきます。

$\bigtriangleup CFH$と$\bigtriangleup AFI$の$\angle CHF$、$\angle AIF$はともに$90^{\circ}$です。そのように作図したので当前ですね。
また、$\angle CFH$と$\angle AFI$は対頂角(向かい合う角)なので、等しいです。
よって、$\angle CHF= \angle AIF$、$\angle CFH= \angle AFI$なので、$\bigtriangleup CFH$と$\bigtriangleup AFI$は2角が等しい。つまり、$\bigtriangleup CFH$と$\bigtriangleup AFI$は相似だと分かりました。
$\bigtriangleup CFH$と$\bigtriangleup AFI$は相似より、各辺の比は等しい
$\bigtriangleup CFH$と$\bigtriangleup AFI$は相似より、各辺の比は等しくなります。
$CH$と$AI$、$CF$と$AF$、残りの$FH$と$FI$がそれぞれ同じ比率になります。

関係性
よって、$CH:AI=CF:AF$となるので、$CH・AF=AI・CF$が成り立ちます。従って、高さ$CH$、$AI$と$CF$、$AF$には、$\displaystyle \frac{CH}{AI}=\frac{CF}{AF}$という関係性があることが分かりました。
$\bigtriangleup BCD$と$\bigtriangleup ABD$の面積比も同じ
高さ$CH$、$AI$と$CF$、$AF$には、$\displaystyle \frac{CH}{AI}=\frac{CF}{AF}$という関係性が分かりました。この関係式を変形することで、面積比も知ることができます。
$\displaystyle \frac{CH}{AI}=\frac{CF}{AF}$の左辺に$\displaystyle \frac{\frac{BD}{2}}{\frac{BD}{2}}$を掛けます。※$\displaystyle \frac{\frac{BD}{2}}{\frac{BD}{2}}=1$なので、掛けても問題ありませんね
(左辺)$\displaystyle =\frac{CH}{AI}\times \frac{\frac{BD}{2}}{\frac{BD}{2}}=\frac{\frac{BD・CH}{2}}{\frac{BD・AI}{2}}$
ここで、下図、青色の三角形と赤色の三角形の面積を思い出してください。

青と赤の三角形の面積は下記の通りでしたよね。
青色の$\bigtriangleup BCD$の面積$\displaystyle \color{blue} S_{bcd} = \frac{BD・CH}{2}$
赤色の$\bigtriangleup ABD$の面積は$\displaystyle \color{red} S_{abd} = \frac{BD・AI}{2}$
これは、先ほどの左辺の分母と分子がそれぞれの面積になっています。
(左辺)$\displaystyle =\frac{\color{blue} \frac{BD・CH}{2}}{\color{red} \frac{BD・AI}{2}}$
よって、
(左辺)$\displaystyle = \frac{\frac{BD・CH}{2}}{\frac{BD・AI}{2}} = \frac{S_{bcd}}{S_{abd}}$
少しまとめます
少しややこしくなってきましたので、少しまとめます。
まず、相似関係より$\displaystyle \frac{CH}{AI}=\frac{CF}{AF}$が分かりました。ここから先ほどまでの計算の流れを式にしますね。
$\displaystyle \frac{CH}{AI}=\frac{CH}{AI} \times \frac{\frac{BD}{2}}{\frac{BD}{2}}$
$\displaystyle =\frac{\frac{BD・CH}{2}}{\frac{BD・AI}{2}}$
$\displaystyle =\frac{S_{bcd}}{S_{abd}}$
$\displaystyle =\frac{CF}{AF}$
つまり、$\displaystyle \frac{CH}{AI}=\frac{S_{bcd}}{S_{abd}}=\frac{CF}{AF}$

青と赤の三角形の面積と$CF$、$AF$との関係性$\displaystyle \frac{S_{bcd}}{S_{abd}}=\frac{CF}{AF}$が分かりました。
スポンサーリンク
$\bigtriangleup ABD$と$\bigtriangleup ACD$から分かること
「$\bigtriangleup ACD$と$\bigtriangleup BCD$から分かること」と全く同じ手順を行うことで、
青と赤の三角形の面積と$AF$、$CF$との関係性$\displaystyle \frac{S_{abd}}{S_{acd}}=\frac{BE}{CE}$が分かりました。
※同じ手順ですが、詳細を書いてほしい場合は、コメントくださいね

$\bigtriangleup ACD$と$\bigtriangleup BCD$と$\bigtriangleup ABD$より
青と赤の三角形の面積と$AG$、$BG$との関係性$\displaystyle \frac{S_{acd}}{S_{bcd}}=\frac{AG}{BG}$が分かりました。
青と赤の三角形の面積と$CF$、$AF$との関係性$\displaystyle \frac{S_{bcd}}{S_{abd}}=\frac{CF}{AF}$が分かりました。
青と赤の三角形の面積と$AF$、$CF$との関係性$\displaystyle \frac{S_{abd}}{S_{acd}}=\frac{BE}{CE}$が分かりました。
以上より、下記3つの式を得ました。
$\displaystyle \frac{S_{acd}}{S_{bcd}}=\frac{AG}{BG}$・・・( i )
$\displaystyle \frac{S_{bcd}}{S_{abd}}=\frac{CF}{AF}$・・・( ii )
$\displaystyle \frac{S_{abd}}{S_{acd}}=\frac{BE}{CE}$・・・( iii )
( i ) と ( ii )の各辺を掛けます。
$\displaystyle \frac{S_{acd}}{S_{bcd}}・\frac{S_{bcd}}{S_{abd}}=\frac{AG}{BG} ・\frac{CF}{AF}$
$\displaystyle \frac{S_{acd}}{S_{abd}}=\frac{AG}{BG} ・\frac{CF}{AF}$・・・ ( iv )
( iv ) と ( iii ) の各辺を掛けます。
$\displaystyle \frac{S_{acd}}{S_{abd}}・\frac{S_{abd}}{S_{acd}}=\frac{AG}{BG} ・\frac{CF}{AF}・\frac{BE}{CE}$
$\displaystyle 1=\frac{AG}{BG} ・\frac{CF}{AF}・\frac{BE}{CE}$
以上で証明終了です。
参考(入れ替えなど不要です)
$\displaystyle 1=\frac{AG}{BG} ・\frac{CF}{AF}・\frac{BE}{CE}$を最初に定理を紹介した、下記に合わせておきます。
$\displaystyle \frac{AG}{BG} \frac{BE}{CE} \frac{CF}{AF} = 1$
$\displaystyle 1=\frac{AG}{BG} ・\frac{CF}{AF}・\frac{BE}{CE}$
両辺入れ替えます。
$\displaystyle \frac{AG}{BG} ・\frac{CF}{AF}・\frac{BE}{CE} = 1$
$\displaystyle \frac{CF}{AF}$と$\displaystyle \frac{BE}{CE}$を入れ替えます。
$\displaystyle \frac{AG}{BG} ・\frac{BE}{CE}・\frac{CF}{AF} = 1$
まとめ
チェバの定理は三角形の外部に点がある場合でも成り立つことが分かりました。
チェバの定理の証明で使った直角三角形とは違い、普通の三角形で証明してみましたが、特に問題がある箇所はありませんでした。
もし、他にも試してほしい形の三角形があれば、コメントください。検証してみます。
それでは、最後までお読みいただきありがとうございました!
キーワード
気になる人はGoogle検索で調べてみてね。
チェバの定理、三角形、相似、対頂角
スポンサーリンク

